
天天一身白衬衣+牛仔裤、为了专心想题走路不戴眼镜……
但又非常擅长社交、3岁就会“整蛊”大人、不止研究搞得好还特别会摄影。
——这样的数学家你见过吗?
他就是今年七月刚刚摘下菲尔兹奖的牛津大学教授詹姆斯·梅纳德 (James Maynard)。

此前因为优化张益唐的“孪生素数猜想”结果一战成名,连华裔数学天才陶哲轩都对初出茅庐的他赞不绝口。
现在,他又拿下了2023科学突破奖下的数学新视野奖,将10万美元奖金收入囊中。
年仅35岁的他,因为在数论领域的多项惊人成就,早就斩获了无数奖项,可谓是年少成名、前途不可估量。
然而有趣的是,他和我们刻板印象里的多数天才数学家、科学家等不太一样,有着非常鲜明的个性。
天才的一些“怪癖”他有,可是把他放进“普通人”群里,又能非常和谐地打成一片。
这究竟是怎样一位数学家?
梅纳德是个“80后”,1987年出生于伦敦。
他在全球排名第一的牛津大学数学专业拿到博士学位,现在是该校的一名教授(他本科和硕士在剑桥大学完成)。
故事要从三岁时讲起。
那年,评估员通过例行幼儿智力检查来到他家,没想到竟被一个“小屁孩”给捉弄了。
在梅纳德看来,评估员给的测试题都太简单,简单到“stupid”。
于是,当这位评估员指着一个牛问他是什么动物时,他故意回答“羊”好观察她什么反应。
然后还没等测试做完,梅纳德就自行宣布结束,拿起乐高开始玩。
无奈的评估员便对他妈说:
你家孩子没规矩(缺乏纪律),上学后怕是有麻烦。
结果梅纳德确实把这种“个性”带到了学校。
有一段时间,他的物理老师对于那种只写出正确答案但没写过程的作答只给1/3的分数。
梅纳德觉得这种评分标准太荒谬了,索性答题时就是不写过程以示抗议(当然,结果都是对的)。
对此,他的老师早就表示无奈了。
梅纳德对自己的评价也是:我就是那种一直在问“为什么为什么为什么”的那种“讨厌鬼”,并且只做自己想做的事情。
后来,等到他博士毕业后去蒙特利尔大学做博士后研究,导师告诫他先不要研究素数问题时(因为已经难倒几个世纪的数学家了),他也完全不听。
但事实证明,他的实力允许他这么“任性”。
对于本次数学新视野奖,官方给出梅纳德的获奖理由是为了表彰他“对解析数论作出的贡献,尤其是素数分布方面”。

提到素数分布,就不得不提到那次让他一战成名的研究,这段故事可以说是一波三折。
虽然几千年前 ,我们就已经知道素数有无穷多个,但是这些素数排布在数轴上的时候,却没有非常明显的规律。
“通常情况下,你顺着数轴的方向看,素数之间的间隔会越来越大,”梅纳德说,”但是孪生素数猜想说,就算从大面上素数的间隔越来越大,也有极少数的素数会互相挨着非常接近。理解素数间隔是理解素数分布最基本的问题。”
数学家们都相信,能找到无穷多的孪生素数,这就是「孪生素数猜想」,虽然听上去简单,但几百年来一直没人能证明。
梅纳德怀疑,改进十年前的一篇论文中描述的过滤素数的方法,可能会找到突破点。
但是,就当梅纳德还在研究时,一位当时还名不见经传的数学家张益唐横空出世,先他一步证明了存在无穷多个素数之差小于7000万的素数对。
一时间,张益唐可以说风头无两,还因此摘下了「数论界最高奖」柯尔奖。
仅仅相隔半年,26岁的梅纳德也拿出了他的研究成果:他提出了一个完全独立的、比张益唐更强大的解决方法,把这一数字缩小到了600。
但就在他准备发表前,又发生了一件对年轻数学家来说很可怕的事:
他和导师从私下里得知,当时已成名许久的菲尔兹奖获得者陶哲轩也在同一问题上,得出了基本相同的结果。
据QuantaMagazine报道,在读过梅纳德的证明方法后,陶哲轩认为,其证明方法比自己的更简洁。
出于惜才之心,陶哲轩主动放弃了与他一同发表这项研究的机会,以免自己的名气掩盖了年轻数学家的成就。
接下来,梅纳德也用自己的努力证明了陶哲轩没有看错人。
作为一个数论学家,他一直致力于研究那些最难的简单问题,除了上面提到的「孪生素数猜想」,他的战绩还有攻下了困扰大家80年的数学难题——Duffin-Schaeffer猜想。
Duffin-Shaeffer猜想是度量丢番图逼近中的一个重要猜想,由物理学家Richard Duffin和数学家Albert Schaeffer在1941年提出。
众所周知,大部分的实数都是π、√2这样的无理数,它们是无法用分数来表示的。
这个猜想假设 f:N→R≥0是具有正值的实值函数,只有当级数:
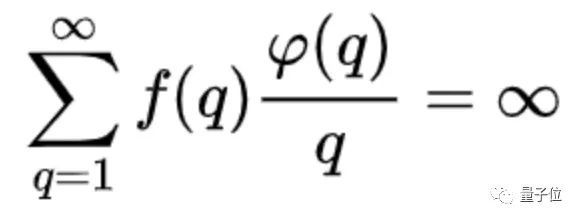
是发散的(q>0,φ(q)为欧拉函数,表示比q小且与q互质的正整数的个数),对于无理数α而言,就存在无穷多个有理数,满足不等式| α-(p/q) |< f(q)/q。
这个证明过程困扰数学家数年,梅纳德和蒙特利尔大学的迪米特里斯·库库洛普洛斯(Dimitris Koukoulopoulos)将它攻破了。

△左一为库库洛普洛斯,右二为梅纳德
在他们的证明中,他们用分母创建了一个图:把分母绘制成图上的点,如果两个点有许多共同的质因数,就用线将两点连接起来。
这样一来,图的结构就编码了每个分母所近似的无理数之间的重叠。原本这种重合度是难以直接测定的。
由此,他们证明了Duffin-Schaeffer猜想的正确性。

Quanta Magazine把这项成果称为“数学领域最罕见的壮举之一”,因为“他们给出了自己研究的领域中基本问题的最终答案”。
由于这些研究成果过于硬核,梅纳德一直广受赞誉,并成为了数论领域最顶级的学者。
牛津大学教授评价他的职业生涯轨迹为“陡峭上升”。
正在写一本关于解析数论的书的作者格兰维尔(Granville )“气愤”地表示:就因为他,我要多写150页,进度严重拖慢。
但有意思的是,詹姆斯·梅纳德家里除了他都是搞人文学科的——他的父母是语言老师,兄弟在学习历史。
他是在牛津大学读研究生时,开始显露出非凡的数学能力。
读到博士后期时,导师Roger Heath-Brown就已经惊呼:
我哪是在指导他,我是跟他合作!我从来没带过这样的学生。
看到这儿,谁也不得不承认这一个不可多得的数学天才。
但其实,有关天才的一些刻板印象在他身上展现的并不多,除了他喜欢几乎天天穿同一套衣服:白衬衣+牛仔裤。
Ps. 有一次去听他演讲的人还搞了个恶作剧,所有人都穿上“梅纳德”套装。

能体现梅纳德“普通人”一面的例子很多。
就比如在孪生素数猜想这个难题中,当他用更厉害的方法得出更小的素数间隙时,一阵兴奋之余,伴随他更多的是下意识的恐惧:是不是自己算错了?
不过,他表示,这种恐惧倒道正是能够极大地激励自己的工作效率。
再比如与不少内向的天才科学家不一样,梅纳德其实很擅长社交,在对外交流中常常展示得健谈、爱笑。
而同事对他的评价也是:热情、有趣和外向。
就在疫情之前,他每天午饭后都会带着自己的咖啡豆到办公室,并为其他数论家煮咖啡。
只不过,从家到办公室的路上他一般选择摘掉眼镜,因为他觉得模糊的视觉可以让自己专注于思考数学题。
这也导致他有次遇到自己妻子都擦肩而过。
——是的,梅纳德已经结婚了,另一半是牛津大学的一位医生。今年他还荣升为“奶爸”。
除此之外,梅纳德的生活也并非只有数学这一件事。
他(曾经)的爱好包括恐龙、天文学和地质学。
他透露,最近几年因为经常去全世界出差参加各种会议,所以开始喜欢上摄影。

△ 梅纳德的摄影作品之一
他去过香港,作为一个不爱早起的人,可以为了拍日出打破惯例。
对于摄影,他现在已接近于痴迷状态。
因为任何东西对于他来说,都是要么完全不喜欢,喜欢上就会钻研到底。
就像他父亲说的一样,梅纳德只有在达到到自己的能力极限后才会放弃。
但,数学还没到这个地步。
接下来,我们不禁也好奇这位特别的天才会继续研究什么方向的课题,是否还会做出同样优秀的成果。
对此,梅纳德本人则说:一切皆有可能。
参考链接:[1]https://www.maths.ox.ac.uk/node/61216[2]https://www.quantamagazine.org/number-theorist-james-maynard-wins-the-fields-medal-20220705/[3]https://arxiv.org/abs/1907.04593[4]https://breakthroughprize.org/Laureates/3/L3932[5]https://www.youtube.com/watch?v=un-z8kgOrV0[6]https://mp.weixin.qq.com/s/vsjFvYZBfYdGf7NM4TgRqg
【相关文章】
★ 华人数学家死磕欧拉方程10年,用计算机找到了让它失效的“奇点”
★ 中国科学院院士成会明:推动废旧锂离子电池材料直接再生回收
★ 潘建伟导师获诺贝尔物理学奖!致辞提及4篇论文都有中国科学家参与
★ 数学天才柳智宇:还俗归来月薪2万,手下败将已成数学家,后悔吗
★ 超3000字,张益唐详细回答零点问题、数学研究、家庭生活
本文地址:https://www.qubaike.com/hotnews/74kueowr.html
声明:本文信息为网友自行发布旨在分享与大家阅读学习,文中的观点和立场与本站无关,如对文中内容有异议请联系处理。







